狄利克雷条件

你知道吗？在数学的世界里，有一种神奇的条件叫做狄利克雷条件。它就像是一把钥匙，能打开函数解析的神秘之门。今天，就让我带你一起探索这个充满魅力的数学世界，揭开狄利克雷条件的神秘面纱吧！

狄利克雷条件的起源

狄利克雷条件，顾名思义，是由德国数学家彼得·古斯塔夫·勒维·狄利克雷提出的。这位数学家在19世纪初，对数学领域做出了巨大的贡献。狄利克雷条件主要应用于数学分析中的傅里叶级数，它要求函数在某个区间内连续，但在该区间的端点处可以不连续。

狄利克雷条件的应用

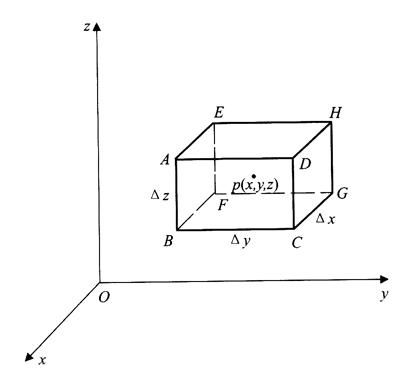
狄利克雷条件在数学分析中有着广泛的应用。比如，在傅里叶级数的收敛性研究中，狄利克雷条件就是一个重要的工具。傅里叶级数是一种将周期函数分解为三角函数之和的方法，而狄利克雷条件则保证了这种分解的准确性。

此外，狄利克雷条件在物理学、工程学等领域也有着重要的应用。例如，在求解热传导问题时，狄利克雷条件可以用来确定边界条件，从而得到问题的解。

狄利克雷条件的特性

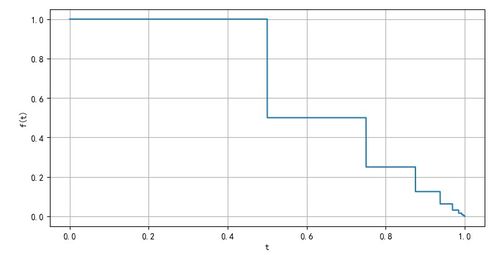
狄利克雷条件具有以下特性：

1. 连续性：函数在某个区间内连续，这是狄利克雷条件的基本要求。连续性保证了函数的稳定性，使得傅里叶级数能够准确地描述函数。

2. 端点不连续性：狄利克雷条件允许函数在区间的端点处不连续。这种不连续性在现实世界中是普遍存在的，如物体的振动、信号的传输等。

3. 周期性：狄利克雷条件要求函数具有周期性。周期性使得函数在某个区间内可以重复出现，从而便于进行傅里叶级数的分解。

狄利克雷条件的挑战

尽管狄利克雷条件在数学分析中有着广泛的应用，但它也带来了一些挑战。首先，满足狄利克雷条件的函数往往比较复杂，求解过程较为繁琐。其次，在某些情况下，狄利克雷条件可能无法保证傅里叶级数的收敛性。

为了解决这些问题，数学家们提出了许多改进方法。例如，通过引入正则化技术，可以使得狄利克雷条件下的函数更加容易求解。此外，通过研究函数的局部性质，可以更好地理解狄利克雷条件下的傅里叶级数。

狄利克雷条件的未来

狄利克雷条件作为数学分析中的一个重要工具，其未来仍然充满挑战和机遇。随着数学、物理学、工程学等领域的不断发展，狄利克雷条件将在更多领域发挥重要作用。

例如，在量子力学中，狄利克雷条件可以用来描述粒子的运动轨迹。在信号处理领域，狄利克雷条件可以帮助我们更好地理解信号的传输和接收过程。狄利克雷条件在未来的发展中，将继续为人类探索未知世界提供有力支持。

说了这么多，你是不是对狄利克雷条件有了更深入的了解呢？这个神奇的数学条件，就像一把钥匙，能打开函数解析的神秘之门。让我们一起期待，在未来的数学世界里，狄利克雷条件将带给我们更多的惊喜吧！